Splain
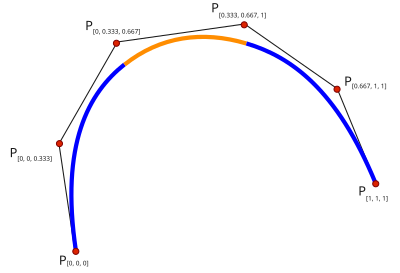
Splain on sile, ühesuguse struktuuriga tükiti polünomiaalne funktsioon, mis liitepunktides rahuldab teatud sileduse tingimusi. Interpolatsiooniprobleemides eelistatakse tihtipeale splain-interpolatsiooni polünomiaalsele interpolatsioonile, kuna see annab sarnaseid tulemusi, isegi kui kasutada madala astme polünoome.[1]
Mõiste "splain" pärineb painduvatest spiraalsetest seadmetest, mida laevaehitajad jajoonestajad kasutavad siledate kujundite saamiseks.[2]
Sissejuhatus
[muuda | muuda lähteteksti]Mõistet "splain" kasutatakse viitamiseks laiale funktsioonide klassile, mis tegeleb andmete interpoleerimise ja/või silumisega. Andmed võivad olla kas ühe- või mitmemõõtmelised. Splainidega lähendamine on tükiti interpoleerimine ühe ja sama astme polünoomiga.[1]
Splain-funktsioonid on olemuselt piiratud mõõtmed, mis on peamine põhjus nende kasulikkuseks arvutustes ja esitustes. Ülejäänud artiklis on keskendutud täielikult ühemõõtmelistele, polünoomsetele splainidele ja kasutatud terminit "splain" selles piiratud tähenduses.
Definitsioon
[muuda | muuda lähteteksti]Lihtsaim splain on tükiti polünomiaalne funktsioon, kus igal polünoomil on üks muutuja. Splain võtab väärtused vahemikust ja määrab need reaalarvude hulka:
Kuna on tükiti määratletud, valime lõiku vahemikus :
Kõik need lõigud on seotud polünoomiga ,
- .
-ndas lõigus vahemikus on määratletud abil,
Antud punkti nimetatakse sõlmedeks. Vektorit nimetatakse splaini sõlme vektoriks. Kui sõlmed on ühtlaselt jaotatud vahemikus siis splaini nimetatakse ühtlaseks, vastasel juhul nimetatakse splaini ebaühtlaseks.[3]
Kui -nda polünoomi tükkidel on iga aste vähemalt , siis splain on astmega (või ).
Kui kehtib punkti naabruses, siis on splain sile (vähemalt) kohal . See tähendab, et kohal jagavad ja ühist tuletisväärtust astmest (funktsiooni väärtusest) kuni astmeni (teisisõnu, kahe kõrvuti asetseva polünoomi tükki ühendavad kõige rohkem sileduse kaotust).
Vektorit kus splainil on siledus kohal nimetatakse splaini sileduse vektoriks.[1]
Näited
[muuda | muuda lähteteksti]Oletame, et intervall on ja alamintervallid on. Oletame, et polünoomi tükid peavad olema astmega ja tükid vahemikus ja peavad ühinema väärtuse ja esimese tuletisega ( korral) samal ajal kui tükid vahemikus ja ühinevad lihtsalt väärtusega ( korral). See määrab splaini tüübi, mille kohaselt
oleks selle tüübi liige ja ka
oleks selle tüübi liige. (Märkus: kuigi polünoomi tükk ei ole ruutpolünoom, siis tulemust kutsutakse ikka ruutsplainiks. See näitab, et splaini astmeks on polünoom-osade maksimaalne aste.) Sellist tüüpi splaini pikendatud sõlme vektor oleks .
Kõige lihtsam splain on astmega . Seda nimetatakse ka astmeliseks funktsiooniks. Järgmine kõige lihtsam splain on astmega . Seda kutsutakse ka lineaarsplainiks.[4] Kinnine lineaarsplain (st esimene ja viimane sõlm langevad kokku) on lihtsalt hulknurk.
Tavaline splain on naturaalne . astme kuupsplain.[5] Sõna "naturaalne" tähendab, et splaini polünoomi teine tuletis on interpoleerimise intervalli lõpp-punktides võrdne nulliga:
Algoritm kuupsplainide arvutamiseks
[muuda | muuda lähteteksti]Kuupsplainid on kujul . Arvestades koordinaatide komplekti soovime leida hulga splainiga
Need peavad rahuldama:
- .
Defineerime ühe kuupsplaini 5-ennikuna kus ja vastavad varem näidatud kujule ja on võrdne parameetriga
Algoritm kuupsplaini arvutamiseks: Sisend: koordinaatide hulk , kus Väljund: splainide hulk, mis koosneb -ist 5-ennikust.
- Loo uus massiiv suurusega ja iga korral seadista
- Loo uued massiivid ja mõlemad suurusega .
- Loo uus massiiv suurusega ja iga seadista
- Loo uus massiiv suurusega ja iga seadista .
- Loo uued massiivid ja kõik suurusega .
- Seadista
- Iga
- .
- .
- .
- Seadista
-
- Loo uus splainide komplekt ja nimeta see valjund_komplekt. Paiguta sinna splaini .
- Iga
- Väljund valjund_komplekt
Viited
[muuda | muuda lähteteksti]- ↑ 1,0 1,1 1,2 Schoenberg, Isaac J. (1946). "Contributions to the Problem of Approximation of Equidistant Data by Analytic Functions: Part A.—On the Problem of Smoothing or Graduation. A First Class of Analytic Approximation Formulae" (PDF). Quarterly of Applied Mathematics. 4 (2): 45–99.
- ↑ Wegman, Edward J., and Ian W. Wright (1983). "Splines in statistics". Journal of the American Statistical Association. 78 (382): 351–365.
{{cite journal}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ Marek Kolk (2012). "Splain-Kollokatsioonimeetod" (PDF). Tartu Ülikool.
- ↑ Tõnu Tõnso. "Splainid" (PDF). Tallinna Ülikool.
- ↑ Helle Trossmann (2004). "Ruut- ja kuupsplainidega interpoleerimine" (PDF). Tartu Ülikool. Originaali (PDF) arhiivikoopia seisuga 18. aprill 2018.
Välislingid
[muuda | muuda lähteteksti]Teooria
- Kuuplsplain moodul Prof. John H. Mathews California State University, Fullerton
- Interaktiivne sissejuhatus splainidesse, ibiblio.org
Exceli funktsioon
Võrguteenuste pakkujad
- Online kuupsplain-interpolatsiooni keskkond
- Õppimine simulatsioonide abil Erinevate kuupsplainide interaktiivne simulatsioon
- Sümmeetrilised splaini kõverad, Theodore Gray animatsioon, The Wolfram Demonstrations Project, 2007.
- Bezieri ja Splaini Kõverate uurimine, interaktiivne veebirakendus
Arvutikood
- Notes, PPT, Mathcad, Maple, Mathematica, Matlab, Holistic Numerical Methods Institute
- mitmesugused rutiinid, NTCC
- Sisl: Opensource C-library for NURBS, SINTEF
- VBA splain-interpolatsioon, vbnumericalmethods.com


![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)

![{\displaystyle S\colon [a,b]\rightarrow \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b75dcb5b39acb84f010daa3cd64628c0afd38e5)

![{\displaystyle [t_{i},t_{i+1}],i=0,...,k-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bc62a7fcb8f1d70c037e2bcd54ae19408d2707b)
![{\displaystyle [a,b]=[t_{0},t_{1}]\cup [t_{1},t_{2}]\cup ...\cup [t_{k-1},t_{k-1}]\cup [t_{k-1},t_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbff5a3b3372ed8ac76920c1946960c9ba17031f)


![{\displaystyle P_{i}\colon [t_{i},t_{i+1}]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5c9ea2b8deebf30d3ab4ff10a89d1810d14c9c8)





















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle [0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5c9e70f7d437509d4ebedb0eaf7ada946e91a79)
![{\displaystyle [0,1],[1,2],[2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56750dc29bca17b184e00d50bd46a1d66af9f743)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2614991ef363710c34e03eb9110d7423e3f60c2)

![{\displaystyle [2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f35c91443ea609dab5936e902226c21c3224919e)














![{\displaystyle C=\left[\left({x}_{0},{y}_{0}\right),\left({x}_{1},{y}_{1}\right),....,\left({x}_{n},{y}_{n}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b031e964d218c37f0e2cc083cadd82545d02846)











































