Kolmnurga võrratus

See artikkel räägib kolmnurga külgede omadusest $z\leq x+y$; teiste kolmnurga omaduste kohta vaata artiklit Kolmnurk

---

Kolmnurga võrratuseks nimetatakse elementaargeomeetrias kolmnurga külgede omadust, mis väidab, et kolmnurga iga kahe külje summa on suurem kui kolmas külg või on sellega võrdne.

Teiste sõnadega kolmnurga küljed $x,y$ ja $z$ on seoses

$z\leq x+y.$

Eukleidese geomeetrias käsitletakse kolmnurga võrratust kauguse teoreemina, kus kasutatakse vektoreid $x$ ja $y$ ning nende pikkusi:

$\|x+y\|\leq \|x\|+\|y\|.$

Eukleidese geomeetria

Joonis 1: Eukleidese kolmnurga võrratuse tõestuseks kasutatud joonis kolmnurgast.

Eukleides tõestas kolmnurga külgede pikkuste võrratust tasapinnalises geomeetrias kasutades joonist 1. Järgnev tõestus on välja toodud Eukleidese raamatus "Elemendid".

Alustatakse kolmnurgaga $\Delta ABC$. Küljele $BC$ moodustatakse võrdhaarne kolmnurk $\Delta BCD$ nii, et külg $BD$ on külje $AB$ pikendus.

Seejärel väidetakse, et nurk $\alpha <\beta$, nii et külg $AD>AC$.

Kuid $AD=AB+BD=AB+BC$, nii et külgede summa on $AB+BC>AC$, mis tõestab kolmnurga külgede pikkuste võrratust.

Võrratusest tulenevad valemid

Võrratus teisel kujul

Võrratusest tulenevalt kehtivad kolmnurga külgede $x,y$ ja $z$ vahel järgmised seosed:

Joonis 2: kolm juhtu kolmnurga võrratuses. Külgede pikkused on $x,y$ ja $z.$

$x+y>z,$ $y+z>x,$ $x+z>y.$

Sellest valemist järeldub

$|x-y|<z,|y-z|<x,|x-z|<y.$

Eelnevatest valemitest tuleneb, et

$|x-y|<z<x+y.$

Seda saab panna kirja valemina

$\max(x,{\text{ }}y,{\text{ }}z)<x+y+z-\max(x,{\text{ }}y,{\text{ }}z),$ mis on sama mis $2\max(x,{\text{ }}y,{\text{ }}z)<x+y+z.$

Kolmnurga võrratuse juhud

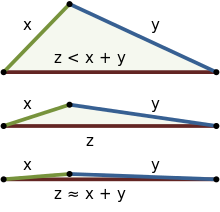
Kui on antud kolm külge $x,y$ ja $z$, kus $z$ on pikim külg, siis tulenevalt $z$-külje pikkusest saab võrratus esineda kolmel kujul:

1. $z<x+y$
2. $z=x+y$(summavektor vektorite käsitluses)
3. $z\approx x+y$, kus $z$-külje pikkus on vähesel määral väiksem kui $x$ ja $y$ summa.

Näide kolmnurga võrratuse kasutamisest

Näide kahel hulknurgal

Olgu meil hulknurk $ABCD$ ja selle sees kolmnurk $\Delta AMD$.

Tõestame, et $P(ABCD)>P(AMD),$kus $P$ on ümbermõõt ehk kõikide külgede summa.

1. Rakendame kolmnurga võrratust kolmnurkadele $\Delta ABM$ ja $\Delta DCM.$
2. Saame $AB+BM>AM$ ja $MC+CD>MD.$
3. Liidame võrratused: $AB+(BM+MC)+CD>AM+MD$ ehk $AB+BC+CD>AM+MD.$
4. Liites võrratuse mõlemale poolele suuruse $AD.$
5. Saame $AB+BC+CD+AD>AM+MD+AD$ ehk $P(ABCD)>P(AMD).$

Kolmnurga võrratus vektorruumis

Joonis 3: kolmnurga võrratus kasutades summavektorit, kus $v$ja $w$ on vektorid.

Kui on antud normeeritud vektorruum $V,$siis üks normi määratlevaks tingimuseks on kolmnurga võrratus:

$\|x+y\|\leq \|x\|+\|y\|\quad \forall \,x,y\in V$

Sellest tuleneb kolmnurga reegel, mis seisneb selles, et geomeetriliste vektorite $x$ ja $y$ summavektoriks $x+y$ nimetatakse vektorit, mis on suunatud vektori $x$ alguspunktist vektori $y$ lõpp-punkti ning summavektori pikkus on väiksem kui $x$ ja $y$ pikkuste summa.

Meetriline ruum

Olgu $X$ mitte tühi meetriline ruum ning $d$ funktsioon $X\times X$üle reaalarvude. Üheks meetrilise ruumi tingimuseks on:

$d(x,y)\leq d(x,z)+d(z,y),\forall x,y,z\in X.$

Igale paarile $x,y\in X$ on vastavusse seatud reaalarv $d(x,y),$mis on $x$ ja $y$ vaheline kaugus: $d(x,y)=|x-y|$(absoluutväärtus või moodul arvude $x$ ja $y$ vahest).

Tõestame antud aksioomi lähtudes kauguse definitsioonist.

$\forall x,y,z\in \ X$ korral:

(M1) $d(x,y)\geq 0;$

(M2) $d(x,y)=|x-y|,$kui $x=y;$

(M3)$d(x,y)=|x-y|=|-(x-y)|=|y-x|=d(y,x);$

(M4) $d(x,y)=|x-y|=|(x-z)+(z-y)|\leq |x-z|+|z-y|=d(x,z)+d(z,y).$

Tagurpidi kolmnurga võrratus

Tuletame meetrilise ruumi $X$eeltoodud aksioomist tagurpidi kolmnurga võrratust.

$\forall x,y,z\in \ X$ korral:

$d(x,y)\leq d(x,z)+d(z,y).$

Teisendame võrratust eelmises peatükis mainituid sammude M3 ja M4 abil:

$d(y,z)\leq d(y,x)+d(x,z)=d(x,y)+d(x,z)$

ja sellest tuleneb

$-d(x,y)\leq d(x,z)-d(y,z)\leq d(x,y)$

ning saame

$|d(x,y)-d(x,z)|\leq d(y,z),$mis on tagurpidi kolmnurga võrratus.

Tagurpidi kolmnurga võrratus omab kuju $|\|x\|-\|y\||\leq \|x-y\|,$kus $\|x-y\|=d(x,y)$ ehk meetrilise (ja normeeritud) ruumi kaugus. Sellest tulenevalt on kolmnurga tõestus järgmine:

$d(x,y)=\|x-y\|=\|(x-z)+(z-y)\|\leq \|x-z\|+\|z-y\|=d(x,z)+d(z,y),$

mis tähendabki seda, et $d(x,y)\leq d(x,z)+d(z,y).$

Tõestame, et tagurpidi kolmnurga võrratus kasutab fundamentaalset kolmnurga võrratust eeldades, et $\|y-x\|=\|-1(x-y)\|=|-1|\|x-y\|=\|x-y\|$:

$\|x\|=\|(x-y)+y\|\leq \|x-y\|+\|y\|\Rightarrow \|x\|-\|y\|\leq \|x-y\|,$

$\|y\|=\|(y-x)+x\|\leq \|y-x\|+\|x\|\Rightarrow \|x\|-\|y\|\geq -\|x-y\|,$

Ning kui paneme mõlemad võrratused kokku, saame

$-\|x-y\|\leq \|x\|-\|y\|\leq \|x-y\|\Rightarrow {\bigg |}\|x\|-\|y\|{\bigg |}\leq \|x-y\|.$

Vaata ka

• Kolmnurk
• Meetriline ruum
• Vektorruum