Kasutaja:Krahh/liivakast

See on kasutaja Krahh liivakast. Kasutaja liivakast on kasutajalehekülje alamleht. Siin kasutaja katsetab või valmistab ette loodavaid artikleid. See ei ole entsüklopeediaartikkel. Enda liivakasti loomiseks klõpsa siia.

Illustration of zero-phonon line and phonon side band. Created by Mark Somoza based on figures in: J. Friedrich and D. Haarer (1984). “Photochemical Hole Burning: A Spectroscopic Study of Relaxation Processes in Polymers and Glasses”. Angewandte Chemie International Edition in English 23, 113-140. — Joonis 1. Illustratsioon üksiku kromofoori neelduvuse spektrist. Kitsam piik on nullfoononriba ning laiem moodustis on foonon külgriba. Kiirgusspektri puhul on foononkülgriba madalamal sagedusel.

Nullfoononriba ja foonon külgriba kujutavad valgust neelavate ja kiirgavate osakeste (kromofooride) joone kuju läbipaistavas tahkes maatriksis. Iga kromofoor annab aine spektrisse nullfoononriba ja foonon külgriba. Kui tegemist on neelduvuse spektriga on foonon külgriba kõrgemal sagedusel ning kiirguse spektris on foonon külgriba madalamal sagedusel kui nullfoononriba.^[1]

Esimesel joonisel on kujutatud tüüpiline üksiku kromofoori nullfoononriba ja foonon külgriba. Nullfoononriba asukoht on ω', mis on määratud elektroni energiatasemete erinevusega ning kromofoori ümbrusega. Sellel joonisel on tegemist elektroni ergastamisega, kuna foonon külgriba on suuremal sagedusel, kui nullfoononriba. α joonisel olevates valemites on Debye-Walleri faktor. Vahet Δ, nullfoononriba ja foonon külgriba vahel, iseloomustab Francki-Cordoni printsiip.^[1]

Energia jaotus nullfoononriba ja foonon külgriba vahel sõltub suuresti temperatuurist. Madalal temperatuuril ei ole piisavalt energiat, et palju foononeid ergastada, aga mida kõrgem on temperatuur seda väiksemaks muutub nullfoonon kiirgumise tõenäosus. Kas toatemperatuuril on nullfoononriba eristatav või mitte oleneb debye temperatuurist.^[1]

Energiatasemed

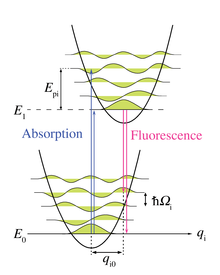
Energy level diagram for transitions between electronic levels with or without photons (alt. vibrations) Created by Mark Somoza based on figures in: J. Friedrich and D. Haarer (1984). “Photochemical Hole Burning: A Spectroscopic Study of Relaxation Processes in Polymers and Glasses”. Angewandte Chemie International Edition in English 23, 113-140. — Joonis 2. Energia diagramm elektroni energiatasemete muutustest. Välja on toodud nii kolme foononiga kui ka foononiteta muutus. Nooled näitavad vasakul neeldumist ning paremal kiirgumist.

Foononitega elektron üleminekut kirjeldab Francki-Cordoni printsiip, mis teeb eelduse, et elektroni ergastamine või relakseerumine elektronkihtide vahel on väga kiire võrreldes võre osakeste nihkumisega. Joonisel 2 on näha energia diagramm energiatasemete ja foononitega. Energiatasemed on märgitud E₀ ja E₁. Foononeid kirjeldatakse lainefunktsioonidega, mida kujutavad rohelised lained. q_i on võre oskeste võnkumise koordinaat. $\hbar \Omega _{i}$ on võre osakese võnkeenergia kvant.^[2]

Esimene nool kujutab koos foononitega absorptsiooni. Foononitega absorptsioonil neelab uurimisobjekt rohkem energiat kui ainult elektroni üleminekul. Antud näite puhul kolm foononit. Teine nool kujutab nullfoonon neeldumist, mis tekitab nullfoononriba. Kolmas nool kujutab fluorestsentsi koos foononitega. Foononitega fluorestsentsi puhul kiirgab uurimisobjekt vähem energiat, kui ainult elektroni üleminekul, kuna osa energiat läheb kiirgumiseta üleminekuks. Antud näite puhul kolm foononit. Neljas nool kujutab nullfoonon relaksatsiooni, mis tekitab nullfoononriba.^[2]

Peale Franck-Cordoni printsiibi eelduse tehakse veel 3 eeldust. Esiteks, et võre võnkumisi kirjeldavad harmoonilised kvantostsillaatorid. Selle rakendamist on näha joonise 2 paraboolsete potentsiaaliaukude puhul. Teine eeldus on see, et ainult kõige madalamal energiatasemel olevaid võre võnkumisi ergastatakse. Kolmas eeldus on see, et vastastikmõju kromofoori ning võre vahel on samasugune nii tava kui ka ergastatud olekus. Seda võib näha joonise 2 ühesuurustest paraboolidest ning foonon tasemete ekvidistantsusest.^[2]

Franck-Cordoni printsiip

Franck-Cordoni printsiip kirjeldab, kui tõenäoliselt toimuvad võnkeenergiate ning elektroni energiate üleminekud. Jooniselt 2 võib seda näha sellest, et foononüleminek toimub kohas, kus võnkeenergia lainefunktsioonid on maksimumis. Ehk ülemineku tõenäosus sõltub foononite lainefunktsioonide kattumisest alg ning lõpp energiatasemetel. Franck-Cordoni printsiip sobib hästi kirjeldama kromofoore. Üks seda printsiibi kasutust piirav eeldus on see, et elektroni ergastamine või relakseerumine elektronkihtide vahel on väga kiire võrreldes võre osakeste nihkumisega. Kuna kromofoorid käituvad analoogselt molekulidega, mille järgi Franck-Cordoni printsiip välja töötati, siis see kehtib nende kohta ning antud printsiipi saab kasutada nende kirjeldamiseks.^[3]

Joone kuju

Nullfoononriba joone kuju kirjeldab Lorentzi funktsioon ning selle laius oleneb kromofoori elueast. Kromofoori eluiga kirjeldab seda, kui kiirelt ergastunud elektronid relakseeruvad ehk kui kaua aine kiirgab peale ergastust. Kui aine eluiga on pikk kiirgab aine aeglaselt ja sellega kaasnevalt ühtlaselt ehk sel on kitsas piik. Kristallvõre kromofoori ümber vähendab selle eluiga, kuna toimub ka kiirgumiseta relakseerumine.^[2]

Foonon külgriba joone kuju kirjeldab Poissoni jaotus, kui on tegemist diskreetse üleminekute kogusega, ehk see kehtib madalatel temperatuuridel. Kõrgetel temperatuuridel kirjeldab joone kuju Gaussi jaotus. Piikide laiust mõjutab homogeenne laienemine, mis tuleneb sellest, et osakeste energiatasemed ei ole kindlad, vaid tõenäosuslikud. Teiseks põhjuseks on mittehomogeenne laienemine, mis tuleneb sellest, et iga identset kromofoori ümbritseb erinev maatriks, mis mõjutab energia kogust, mida läheb vaja elektroni energiataseme muutuseks. Sellest tulenevalt on üksikud nullfoononribad ja foonon külgribad nihkes ja kattuvad, mis põhjustab piikide laienemise. Homogeenne ning mittehomogeenne laienemine teevad laiemaks mõlemat joont.^[1]

Debye-Waller

Debye-Walleri faktor iseloomustab tõenäosust, et ühe osakese hajumine teiselt osakeselt, mis on osa keerulisest süsteemist, on elastne ega muuda komplekse süsteemi olekut. Kuna nullfoononriba koosneb sellistest osakestest iseloomustab see faktor nullfoononriba ja foonon külgriba omavahelist suhet. Mida väiksem on Debye-Walleri faktor seda väiksem on nullfoononriba võrreldes foonon külgribaga. Antud faktor väheneb temperatuuri tõusmisega. Seda faktorit kasutades saab igale materjalile arvutada temperatuuri, millest alates materjali normaalvõnkumised on maksimaalse energiaga. Seda temperatuuri nimetatakse Debye temperatuuriks.^[4]

Debye temperatuurist oleneb, kui kõrgel temperatuuril on nullfoononriba veel nähtav. Mida madalam on keskkonna temperatuur võrreldes Debye temperatuuriga seda väiksem on tõenäosus foonon üleminekuks. Sellise aine jaoks nagu teemant, millel on debye temperatuur 2000K juures, on toatemperatuur madal temperatuur ning paljude kromofooride nullfoononribad on toatemperatuuril nähtavad. See tuleneb teemandi jäigast struktuurist, kuid teemant on erand ning enamus ainete jaoks on toatemperatuur kõrge temperatuur.^[4]

Kasulikkus

Nullfoononribad on kitsad, intensiivsed ning karakteersed piigid. Samuti reageerivad need tugevasti keskkonna tingimustele nagu näiteks temperatuur, pinge või elektriväli. Tänu sellistele omadustele on materjalidel, millel on hea nullfoononriba, perspektiivi leida kasutust erinevates sensorites, bioobjektide kujutamises või mikromaailma uurimises.^[5]

Viited

↑ ^1,0 ^1,1 ^1,2 ^1,3 J.J.Friedrich, D. Haarer cite; 1984; "Photochemical Hole Burning: A Spectroscopic Study of Relaxation Processes in Polymers and Glasses"; Angewandte Chemie International Edition in English, volume=23, issue= 23, pages=113–140
↑ ^2,0 ^2,1 ^2,2 ^2,3 Silʹd, O.; 1988; "Zero-phonon lines and spectral hole burning in spectroscopy and photochemistry"; Berlin, Springer-Verlag, pages=1-36
↑ J.Franck; 1926; "Elementary processes of photochemical reactions"; Transactions of the Faraday Society, issue=21; pages=536–542
↑ ^4,0 ^4,1 Harry J. Lipkin; Physics of Debye-Waller Factors; artikkel
↑ Abdelghani Laraoui, Halley Aycock-Rizzo, Yang Gao, Xi Lu, Elisa Riedo, Carlos A. Meriles; 2015; "Imaging thermal conductivity with nanoscale resolution using a scanning spin probe"; Nature Communications; artikkel

[:0-1] 1,0 ^1,1 ^1,2 ^1,3 J.J.Friedrich, D. Haarer cite; 1984; "Photochemical Hole Burning: A Spectroscopic Study of Relaxation Processes in Polymers and Glasses"; Angewandte Chemie International Edition in English, volume=23, issue= 23, pages=113–140

[:1-2] 2,0 ^2,1 ^2,2 ^2,3 Silʹd, O.; 1988; "Zero-phonon lines and spectral hole burning in spectroscopy and photochemistry"; Berlin, Springer-Verlag, pages=1-36

[3] J.Franck; 1926; "Elementary processes of photochemical reactions"; Transactions of the Faraday Society, issue=21; pages=536–542

[:2-4] 4,0 ^4,1 Harry J. Lipkin; Physics of Debye-Waller Factors; artikkel

[5] Abdelghani Laraoui, Halley Aycock-Rizzo, Yang Gao, Xi Lu, Elisa Riedo, Carlos A. Meriles; 2015; "Imaging thermal conductivity with nanoscale resolution using a scanning spin probe"; Nature Communications; artikkel

[1]

[2]

[3]

[4]

[5]